前言
去年三月疫情爆发之后开始每天完成LeetCode的daily challenge,六月入职之后搁浅,今年一月重新拾起;近期手感不错,决定参加一次传说中大佬云集的周赛,并顺便拉上了@yo1995,于2021年3月27日美东时间22:30准时举行。特写此文以留念+复盘。
第一题
https://leetcode.com/contest/weekly-contest-234/problems/number-of-different-integers-in-a-string/
不得不说,题干是真的长,不知道那些一分多钟AC的是怎么做到的……紧张的我第一遍就把题读错了,幸亏没点提交,要不然不知道要被罚多少时长。
我当时想出来的比较trivial的做法就是从前往后遍历,遇到数字就记下并继续,遇到字母就停止并把这个数存到hashset里。对于如何初始化num浪费了不少时间,贴一下我的做法:
class Solution:
def numDifferentIntegers(self, word: str) -> int:
s = set()
num = -1
for c in word+'#':
if c.isdigit():
if num == -1:
num = 0
num = num * 10 + int(c)
elif num != -1:
s.add(num)
num = -1
return len(s)
赛后跟yo1995复盘的时候发现他果然用了re,但他是用字母split的,于是我试了一下直接按数字匹配:
class Solution:
def numDifferentIntegers(self, word: str) -> int:
return len(set([int(x) for x in re.findall('\d+', word)]))
我真是tql!
另外的思路:
把字母替换成空格,然后按空格split: https://leetcode-cn.com/u/lucifer1005/
class Solution:
def numDifferentIntegers(self, word: str) -> int:
chars = list(word)
for i in range(len(chars)):
if not chars[i].isnumeric():
chars[i] = ' '
nums = ''.join(chars).split()
return len(set(map(int, nums)))
还有https://leetcode.com/awice/这位大哥的groupby,给跪。。
class Solution(object):
def numDifferentIntegers(self, word):
seen = set()
for k,grp in groupby(word, key=lambda c: c.isdigit()):
if k:
s = "".join(grp)
seen.add(int(s))
return len(seen)
第二题
https://leetcode.com/contest/weekly-contest-234/problems/minimum-number-of-operations-to-reinitialize-a-permutation/
这题好坑,我在草稿纸上划拉了半天,试图找出一个递推关系,后来发现只要按题干描述的方法愣搞就可以。。
class Solution:
def reinitializePermutation(self, n: int) -> int:
cnt = 1
perm = list(range(n))
x = perm
while True:
x = [x[i // 2] if i % 2 == 0 else x[n // 2 + (i - 1) // 2] for i in range(n)]
if x == perm:
break
cnt += 1
return cnt
此题学到的lesson:不要高估某些题目,当数学看起来太复杂的时候,不如试试愣搞……
第三题
https://leetcode.com/contest/weekly-contest-234/problems/evaluate-the-bracket-pairs-of-a-string/
这其实是我觉得最简单的一道题,只要把括号及中间的key按照knowledge那个map替换了就好。我的做法是用一个Boolean变量open记录当前括号的状态:
class Solution:
def evaluate(self, s: str, knowledge: List[List[str]]) -> str:
d = {k:v for k,v in knowledge}
res = ""
open = False
for char in s:
if not open:
if char != '(':
res += char
else:
open = True
word = ''
else:
if char != ')':
word += char
else:
open = False
if word in d:
res += d[word]
else:
res += '?'
return res
前十名里的做法是,只要遇到左括号,就找到下一个右括号,然后处理两者中间的字符。我来试着自己写一下:
class Solution:
def evaluate(self, s: str, knowledge: List[List[str]]) -> str:
d = {k:v for k,v in knowledge}
res = ""
i = 0
while i < len(s):
if s[i] == '(':
j = i + 1
while s[j] != ')':
j += 1
key = s[i+1:j]
res += d[key] if key in d else '?'
i = j+1
else:
res += s[i]
i += 1
return res
第四题
https://leetcode.com/contest/weekly-contest-234/problems/maximize-number-of-nice-divisors/
三十多分钟做完前三题后,终于来到了最后一题。这个题干着实给我看懵了,经过一通冷静分析,我发现可以把题目改写成下边这个问题:
对于正整数primeFactors(以下简称pf),找出pf个可以重复的质数,使他们能组合出的乘积的数量最多
例:pf=5, 选取质数[2,2,5,5,5],此时共有2(质数2的数量)*3(质数5的数量)=6种组合,返回6
例2:pf=8,选取质数[2,2,3,3,3,5,5,5],此时共有2*3*3=18种组合。
于是,此题可以进一步简化为:
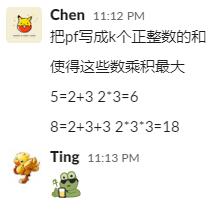
我可真他娘的是个小天才。此时cht选手展现出了惊人的数学直觉,而我并没有理会,开始闷声搞DP,即对于pf,找到pf=a+b使得dp[a]*dp[b]最大。这个方法是行得通的,问题在于O(n^2)的时间复杂度会超时。
 直到我发现了这几个链接知乎、力扣,才发现cht的“多分3”的贪心算法是对的,然而我发现下边的这个写法依旧会超时……
直到我发现了这几个链接知乎、力扣,才发现cht的“多分3”的贪心算法是对的,然而我发现下边的这个写法依旧会超时……
quotient, remainder = divmod(n, 3)
if remainder == 0:
return 3 ** quotient % (10 ** 9 + 7)
elif remainder == 1:
return 3 ** (quotient - 1) * 4 % (10 ** 9 + 7)
else:
return 3 ** quotient * 2 % (10 ** 9 + 7)
此时比赛时间已所剩无几,就在我疯狂尝试改进这个乘方的写法以避免TLE之时,另一位选手完成了绝杀:
所以还是我太菜了啊。a ** b % M会超时的情况下,可以用pow(a, b, M)。写了这么多年Python,竟然不知道pow可以算模。

总结

欢声笑语打出了GG。
从结果来看,第一次参加周赛35min一遍过掉了前三题不算太糟,但其实从审题到效率都还有很大的提高空间;
要说经验教训的话,有的时候不要头太铁(Q2),简单的题目不要想得太复杂。当然最后一题这种其实就是随缘了,梦里无时也是强求不来的。
我们下周同一时间再见!
